Juliaでボックス・ミュラー法を実装する

Juliaでボックス・ミュラー法を実装する

Julia

最近「ゼロからできるMCMC」を読んでいます。Chapter2で、ガウス乱数を発生させる方法として、ボックス・ミュラー法が登場します。

実際にJuliaで実装してみたので、（自分の）記録として残しておきます。

ボックス・ミュラー法

ボックス・ミュラー法は、ガウス乱数を発生させる方法です。

$$
x = \sqrt{(-2 logp)}*coś(2 \pi q)
$$

$$
y = \sqrt{(-2 logp)}*sin(2 \pi q)
$$

ボックス・ミュラー法をJuliaで実装する

実装してみるとこんな感じです。今回は、任意の個数（n）の一様乱数のベクトル（x, y）を発生させて、それにボックス・ミュラー法の関数を当てています。

肝としては、ベクトルに関数を適用してもうまく走らない（例：f_x(p, q)）ので、この様にf_x.(p, q)、関数のあとに「.」（ドット）をつける必要があります。

# ライブラリ
# using Pkg
# Pkg.add("RDatasets")
# Pkg.add("StatsPlots")
using Statistics, StatsPlots

## 初期設定（Wikipediaより）
n = 100000 # 乱数を発生させる個数
p = rand(n)
q = rand(n)

# 関数を定義する
# xを生成する関数
function f_x(p, q)
    sqrt(-2*log(p))*cos(2*π*q)
end

# yを生成する関数
function f_y(p, q)
    sqrt(-2*log(p))*sin(2*π*q)
end

# 実行する
x = f_x.(p, q)
y = f_y.(p, q)

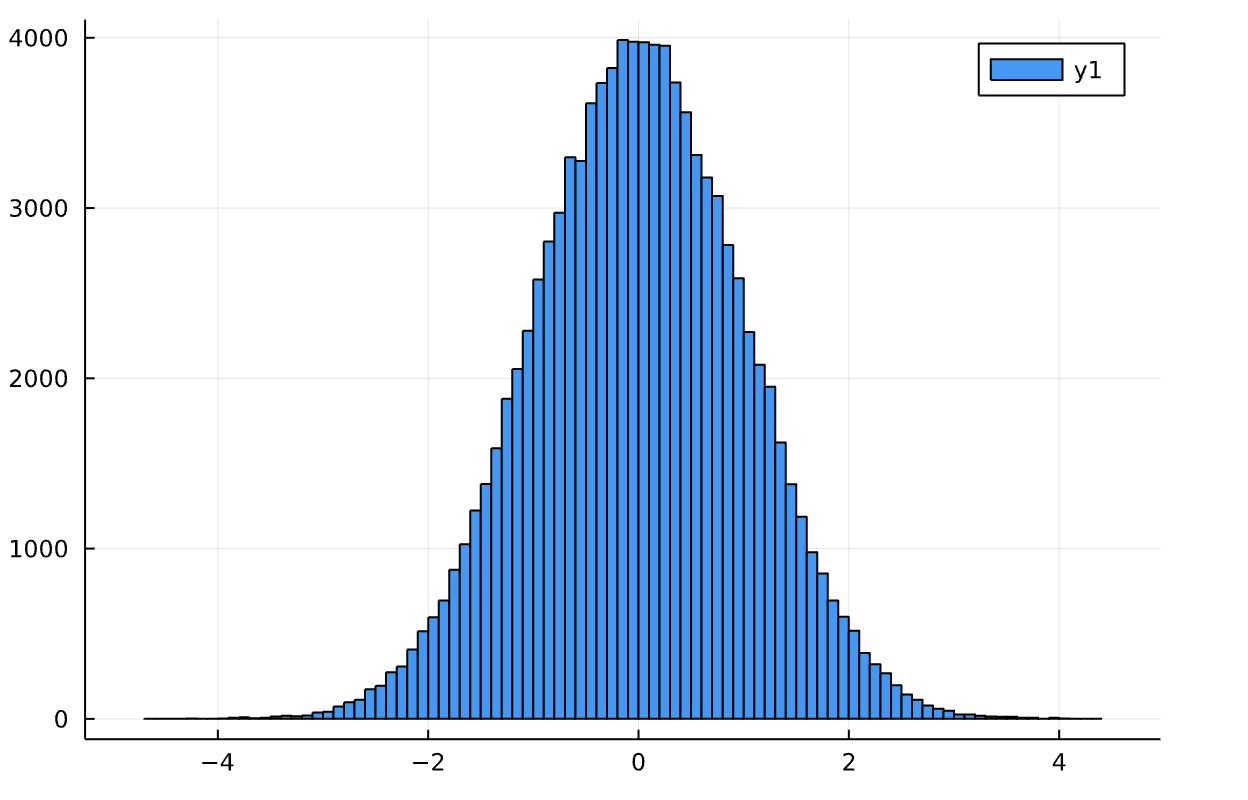
histogram(x)
histogram(y)

ボックス＝ミュラー法 - Wikipedia
ja.wikipedia.org