Rと数値シミュレーションを用いて、ロジスティック回帰分析のサンプルサイズ設計をしようとした所、思った以上に時間が掛かることがわかりました。
RでもdoParallelなどを用いて高速化は可能ですが、それでもやっぱり限界があります。ふと、Juliaで書き直したらどれくらい高速化されるのか気になったので、試してみました。
なお、この記事のコードは「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」の第6章を参考にしています。

Amazonで小杉 考司, 紀ノ定 保礼, 清水 裕士の数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計。アマゾンならポイント還元本が多数…
amzn.asia
↑アフィリエイトリンクではないので、是非買ってください。
実行した環境
- PC: MacBook Air
- CPU: M2
- RAM: 8GB
Juliaで実装する
## パッケージがない場合は追加
# using Pkg
# Pkg.add("Distributions")
# Pkg.add("DataFrames")
using Distributions, Random, GLM, DataFrames
function t2e_logistic(alpha, b0, b1, n, iter_t2e)
# ロジスティック関数
function logistic(x)
return 1/(1+exp(-x))
end
# 有意かどうかを判断
function apply_condition(x)
return ifelse(x < alpha, 0, 1)
end
X = append!(fill(0, n), fill(1, n))
pvalue = fill(NaN, iter_t2e)
d1 = Binomial(1, logistic(b0))
w1 = rand(d1, n)
d2 = Binomial(1, logistic(b0 + b1))
w2 = rand(d2, n)
for i = 1:iter_t2e
Y = append!(rand(d1, n), rand(d2, n))
data = DataFrame(Y = Y, X = X)
fit = glm(@formula(Y ~ X), data, Binomial(), LogitLink())
pvalue[i] = coeftable(fit).cols[4][2]
end
# 配列内の各要素に条件を適用する
result = apply_condition.(pvalue)
return mean(result)
end
## 実行する
t2e_logistic(0.05, 0, 0.2, 100, 200000)
数値シミュレーション本のコードを参考に、Juliaに書き換えて見るとこんな感じ。Juliaはほとんど書いたことがない初心者なので、もっと良い書き方があるかもしれません。
実際に走らせてスピードを比較
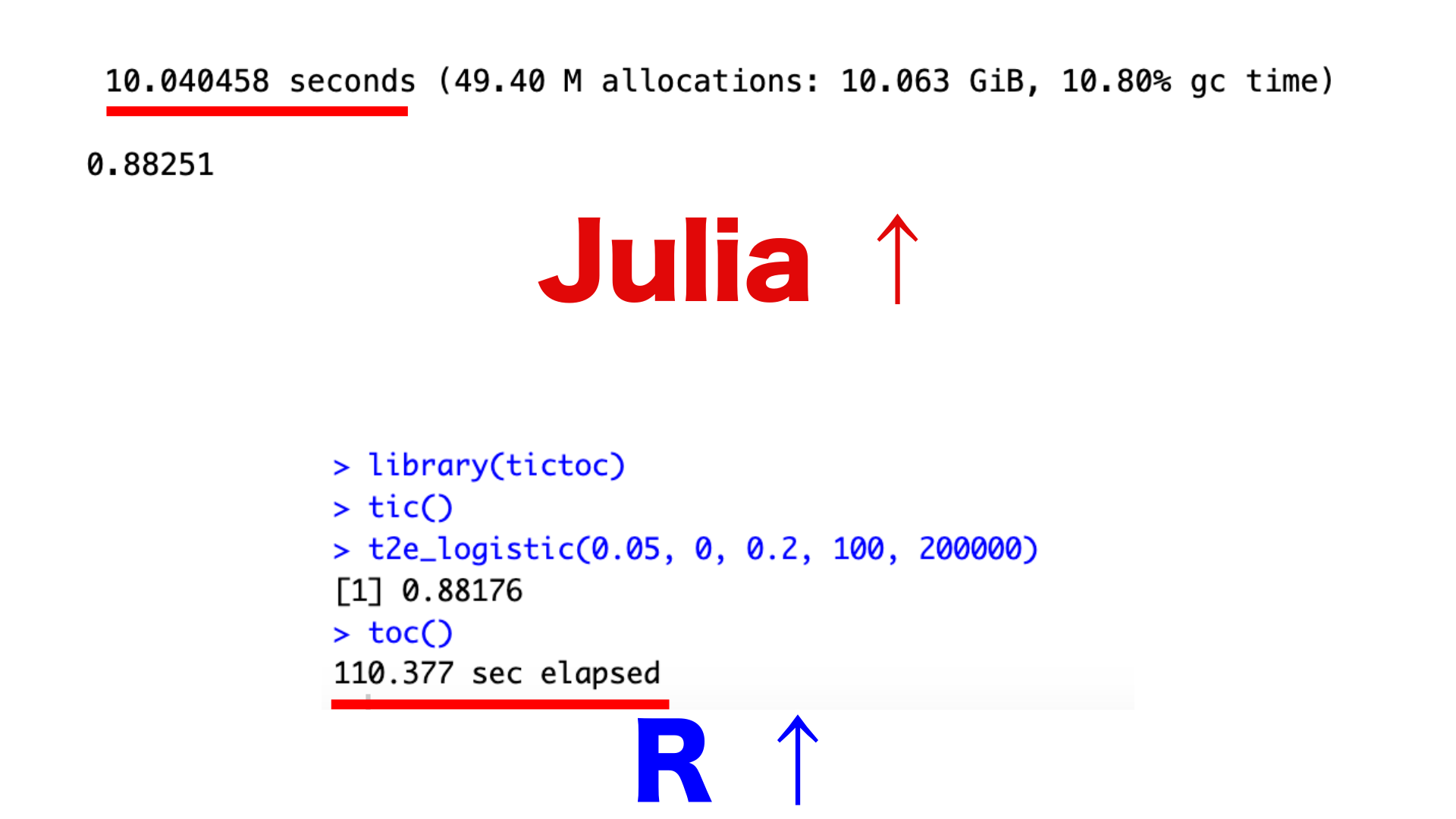
同じ設定で回したところ、Juliaは10秒、Rは110秒と11倍の差に。別の設定で回しても、Juliaが6.7秒で、Rが44秒だったり、34秒に対して259秒だったりと、大きく差は開きました。
もちろんdoParallelなどで並列化すればRでも高速化できますが、Juliaなら素の状態でも非常に速く、更に並列化で高速化も可能。
比較的RやPythonに近い形でここまで高速化できるのであれば、Juliaを触っておく価値はありそうです。特にマルチレベルモデルなどモデルが複雑になればなるほど、計算時間が掛かるので、Juliaを覚えると便利かもしれないと思い始めています。
