Stan Advent Boot Camp 第4日目 重回帰分析をやってみよう

この記事はStan Advent Calendar2020の4日目の記事です。

第1日目：Stanの導入
第2日目：Stanコードの構造と基本的な書き方
第3日目：平均値を推定してみよう

4日目は、Stanで単回帰・重回帰分析のコードを書いてみようというテーマです。

今回使用するデータ・分析・目的

データ

今回分析に使用するデータは、プロ野球データFreakから取得した2019年の打者成績と2020年の推定年俸のデータ。それぞれ規定打席1/3をクリアしている打者を対象にしています。

ただし、データ取得の都合上（そこまで移籍情報を追えていない）、2020年に他チームへ移籍した選手や規定打席1/3に満たない選手についてはデータを除外しています。

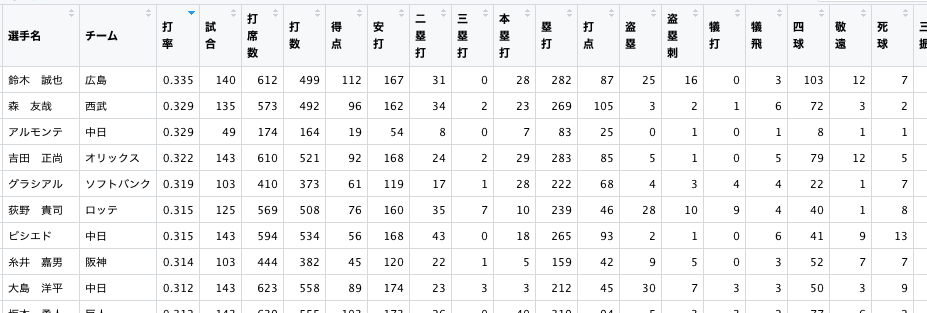
今回分析するデータの一部抜粋。基本的に2020年度の成績が2020年の年俸になるのではなく、2019年の成績によって2020年度の年俸が決定されます。そのため、打者成績はあえて2019年度のものを取得しています。

使用変数・分析目的

• 目的変数：年俸
• 説明変数：打率、本塁打（ホームラン）、盗塁
• 年俸を予測する

変数は打率や安打数、打点など挙げればきりがない程、色々な変数があります。今回は、あくまでStanで重回帰分析を行うことが目的なので、予め使用変数を絞っています。

分析目的は、年俸を予測すること。一番年俸に響きそうな、打率と本塁打（ホームラン）数、そして適当に選んだ盗塁数を説明変数として使用します。

注意：察しの良い方はお気づきかもしれませんが、目的変数である年俸は、正規分布ではありません。しかし、Stanで重回帰分析を行うのが主目的であり、説明の簡略化のために、正規分布とみなした上で分析を行います。辻褄合わせのために、記事の最後で別の分布を当てはめたモデルについて紹介しています。

単回帰分析：打率は年俸を予測するか

単回帰分析とは

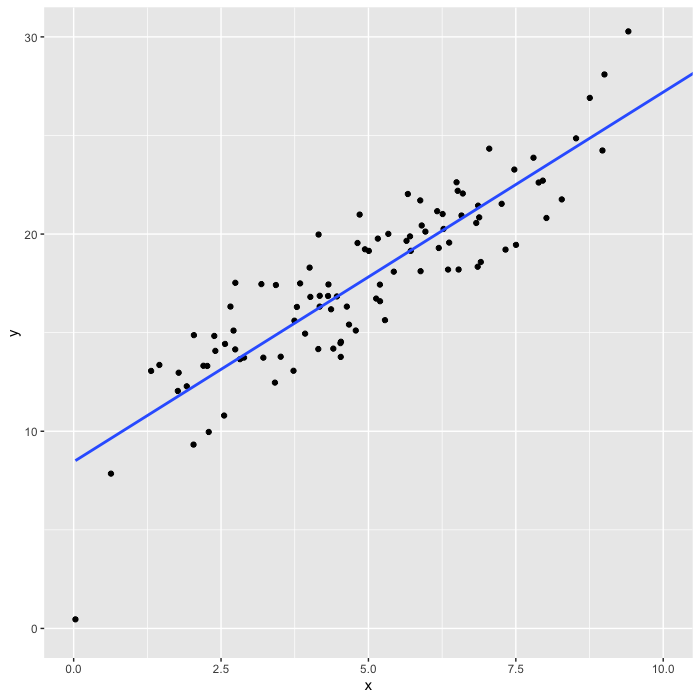
目的変数\(Y\)を説明変数\(X\)で、どれだけ説明できるかということを調べるときに使うのが、単回帰分析です。データを使って上記の回帰直線の形を求めようというのが目的。

$$Y = a + bX$$

先程の図の回帰直線は、一次方程式の形で表されます。\(Y\)と\(X\)の関係は非常にシンプルな形で表されます。このとき、\(a\)が切片、\(b\)が回帰係数になります。

今回の場合、打率\(X\)がどのくらいになれば、年俸\(Y\)はいくらになるのかを、分析して調べるのが目標です。それ表す指標が\(b\)が回帰係数で、Stanで求めたいものになっています。

モデル式

\(Y = a + bX\)だけで表せたらシンプルなのですが、現実はそうは行きません。打率が高くても年俸が引くかったり、逆に打率が低くても年俸が高いこともあり、一定数ばらつきが生じます。具体的には、ホームランバッターは3割以下の打率でも本塁打を打つので、年俸が高くなるというのがいい例ですね。

$$Y = a + bX + \varepsilon[n]$$
$$\varepsilon \sim Normal(0, \sigma)$$
そのため、ばらつきを表現するために、正規分布を使って説明をすることを試みます。\( \varepsilon \)がノイズの項を示し、これが正規分布に従うと仮定します。

$$Y[n] \sim Normal(a + bX[n], \sigma)$$
途中の式展開は省きますが、一人ずつのデータが平均\(a + bX[n]\)、分散\( \sigma)\)の正規分布に従うと考えます。これをStanに落とし込んでいきます。

Stanで実行する

data {
  int<lower=0> N; //人数
  real X[N]; //打率
  real Y[N]; //年俸
  real sd_x; //打率の標準偏差:事前分布のパラメータ①
  real sd_y; //年俸の標準偏差:事前分布のパラメータ②
  real mean_y; //年俸の平均値:事前分布のパラメータ③
}

parameters {
  real a;
  real b;
  real<lower=0> sigma;
}

model {
  for(n in 1:N){
    Y[n] ~ normal(a + b*X[n], sigma);
  }
  a ~ normal(mean_y, 2.5*sd_y);
  b ~ normal(0, 2.5*sd_y/sd_x);
  sigma ~ exponential(1/sd_y);
}

上で紹介したモデル式を、そのままStanに書きます。modelブロックに、先程紹介していたモデル式\( Y \sim Normal(a + bx, \sigma) \)がそのまま記載されているのがわかります。

modelブロックにメインとなるモデル式を記載。そのモデル式において、データと推定するパラメータを見極めた上で、dataブロックとparametersブロックを埋めていくとStanコードが書きやすいです。

modelブロックの\( a \sim\)、\( b \sim\)、\( sigma \sim\)はそれぞれ事前分布。本記事では特に明記されていない限り、Gelman et al.(2020)に基づいて設定しています。

stan_data = list(
  N = nrow(baseball_df),
  X = baseball_df$打率,
  Y =baseball_df$salary
)
stanmodel <- stan_model("2020_Stan_adcal/lm.stan")
fit_stan01 <- sampling(
  stanmodel,
  data = stan_data,
  seed = 1234,
  chain = 4,
  cores = 4,
  iter = 2000
)

Stanコードの細かな実行の仕方については説明を省きますが（詳細な説明は昨日の記事）、上記のコードでStan用のデータを作成、コンパイル、実行が行なえます。

RStanで単回帰分析を実行した結果がこちら。打率は基本小数点単位で変化するので、10で割ると、打率が0.1上がると年俸が約1.6億円上昇していることがわかります。

今回は長くなってしまうため省略しますが、昨日の記事をみて、事後の収束チェックや事後分布の確認を行っておきましょう。

Rで実行する

fit_01 <- lm(salary ~ 打率, data = baseball_df, method = "ml") 
summary(fit_01)

一応Rのlm関数で行った結果を紹介しておきます。目的変数と説明変数を上記のコードの通りに書き、データを指定するだけで分析が実行できます。

Rで単回帰分析を行った結果がこちら。RStanとだいたい同じですね。

重回帰分析

2つ以上の説明変数で、目的変数がどれほど予測できるのか知りたいという場合に利用するのが、重回帰分析です。

モデル式

$$年俸[n] = b_1 + b_2打率[n] + b_3ホームラン数[n] +b_4盗塁数[n] + \varepsilon[n]$$

$$ \varepsilon[n] \sim Normal(o, \sigma)$$
単回帰分析同様、確率分布を使用したモデル式で表現してみます。ノイズのない一番単純なモデルは\( 年俸[n] = b_1 + b_2打率[n] + b_3ホームラン数[n] +b_4盗塁数[n] \)です。これに残差\( \varepsilon \)が追加されます。この式をシンプルにすると、

$$\mu[n] = b_1 + b_2打率[n] + b_3ホームラン数[n] +b_4盗塁数[n]$$

$$年俸[n] \sim Normal(\mu[n], \sigma)$$
このような形で表現されます。単回帰分析と同じく\( \mu \)の中に式を書くことはできますが、可読性向上のために別途まとめています。
このモデル式をStanコードに落とし込んでいきます。

Stanで重回帰分析

data {
  int<lower=0> N;
  real avg[N]; //打率
  real hr[N]; //本塁打
  real st[N]; //盗塁
  real Y[N]; //年俸
  real sd1_x; //打率の標準偏差、事前分布のパラメータに使用
  real sd2_x; //本塁打の標準偏差、事前分布のパラメータに使用
  real sd3_x; //盗塁の標準偏差、事前分布のパラメータに使用
  real sd_y; //年俸の標準偏差、事前分布のパラメータに使用
  real mean_y; //年俸の平均、事前分布のパラメータに使用
}

parameters {
  real a;
  real b[3];
  real<lower=0> sigma;
}

transformed parameters{
  real mu[N];
  for(n in 1:N){
    mu[n] = a + b[1]*avg[n] + b[2]*hr[n] + b[3]*st[n];
  }
  
}

model {
  for(n in 1:N){
    Y[n] ~ normal(mu[n], sigma);
  }
  a ~ normal(mean_y, 2.5*sd_y);
  b[1] ~ normal(0, 2.5*sd_y/sd1_x);
  b[2] ~ normal(0, 2.5*sd_y/sd2_x);
  b[3] ~ normal(0, 2.5*sd_y/sd3_x);
  sigma ~ exponential(1/sd_y);
}

単回帰分析と同じ様に、確率分布（正規分布）をモデル部分に表現しています。\( 年俸[n] \sim Normal(\mu[n], \sigma) \)が、Y[n] ~ normal(mu[n], sigma);として表現されています。また\( \mu = \)の式をtransformed parametersに記載し、データとパラメータをそれぞれのブロックに書いています。

stan_data = list(
  N = nrow(baseball_df),
  avg = baseball_df$打率,
  hr = baseball_df$本塁打,
  st = baseball_df$盗塁,
  Y = baseball_df$salary,
  sd1_x = sd(baseball_df$打率), //事前分布用
  sd2_x = sd(baseball_df$本塁打),
  sd3_x = sd(baseball_df$盗塁),
  sd_y = sd(baseball_df$salary),
  mean_y = mean(baseball_df$打率),
  
)
stanmodel2 <- stan_model("2020_Stan_adcal/MLM.stan")
fit_stan02 <- sampling(
  stanmodel2,
  data = stan_data,
  seed = 1234,
  chain = 4,
  cores = 4,
  iter = 2000
)

回帰係数が増えただけ、事前分布のパラメータが増えていますが、基本は単回帰分析の時と同じ。b[1]が打率の回帰係数なので確認しておくと、だいたい1割上がるごとに9000万円上がっていることがわかります。

これを実行した結果がこちら。

Rで重回帰分析

fit_02 <- lm(salary ~ 打率 + 本塁打 + 盗塁, data = baseball_df) 
summary(fit_02)

Rのlm関数でも同様に重回帰分析を実行することができます。b[1]が打率、b[2]がホームラン、b[3]が盗塁になります。打率が依然として年俸に対して大きな効果をもっています。盗塁数の影響は少なそうです。

ベクトル化を使用してオシャレに重回帰分析

ここまでで、重回帰分析を実行することができました。しかし、あくまで3つの説明変数を使用する場合でしか上記のコードは使用できません。説明変数を2つに減らしたり、4つや5つに増やすとなると、コードを書き換える必要が出てきます。そのたびにStanコードを書いて、コンパイルをするのは非常に面倒です。

そこで、ベクトル化を用いて、一つのStanコードで様々な数の変数に対応した重回帰分析のコードを書いてみます。回帰係数などをvector型で書き直すことにより、可読性の向上（追記：数学的な理解があれば）や高速化に繋がります。

モデル式

$$ \mu = b_1 + b_2 x_1 + b_3 x_2 + \cdots + b_D x_D$$
$$ Y \sim Normal(\mu, \sigma)$$
先程まで紹介していた重回帰のモデルの一人分を数式で表します。わかりやすさために、打率や年俸などを含んでいたモデル式の説明変数を\(x\)に置き換えて一般化しました。この重回帰分析のモデルを線形代数を使って書き換えることを試みます。

$$\boldsymbol{b}^T = (b_0, b_1, b_2, \cdots, b_D) $$
まず、回帰係数\(b\)をベクトルで書きます（上付きTは転置行列を表す）。Dは変数の数を表します。
$$ \boldsymbol{x}^T = (1, x_1, x_2, \cdots, x_D) $$
説明変数\(x\) (1は切片、打率(\(x_1\))、ホームラン数(\(x_2\))、盗塁(\(x_3\)) etc…が入る)についても同様にベクトルで宣言していきます。
$$\begin{eqnarray} \hat{y} &=& b_0 + b_1 x_1 + b_2 x_2 + \cdots b_D x_D \\\\ &=& (b_0, b_1, b_2, \cdots, b_D) \left( \begin{array}{c} 1 \\ x_1 \\ x_2 \\\vdots \\ x_D \end{array} \right) \\\\ &=& \boldsymbol{b}^T \boldsymbol{x} \end{eqnarray}$$
これらを使用して一人目のモデル式をベクトルで表現してみました。いっぱい足し算と掛け算が合った最初のモデル式が、コンパクトになりました。これをN人分のデータに拡張して、

$$\begin{eqnarray} \left( \begin{array}{c} \hat{y}_2 \\ \hat{y}_2 \\\vdots \\ \hat{y}_N \end{array} \right) &=& \begin{pmatrix} 1 & x_{11} & x_{12} \cdots x_{1D} \\ 1 & x_{21} & x_{22} \cdots x_{2D} \\ \\\vdots & & \vdots \\ 1 & x_{N1} & x_{N2} \cdots x_{ND} \end{pmatrix} \left( \begin{array}{c} b_1 \\ b_2 \\ b_3 \\\vdots \\ b_D \end{array} \right) \end{eqnarray}$$

$$ \boldsymbol{\mu} = \boldsymbol{x} \boldsymbol{b} $$

重回帰分析を行列で表すと、このような式になります。\( \hat{y} = b_0 + b_1 x_1 + b_2 x_2 + \cdots b_D x_D \)と説明変数が増えるにつれ長くなっていた式を、\( \boldsymbol{\hat{y}} = \boldsymbol{x} \boldsymbol{b} \)という短く表現することができました。

細かな式展開については「ガウス過程と機械学習」を参照してください。

Stanで実行する

data {
  int<lower=0> N; //人数
  int<lower=0> K; //変数の数
  matrix[N, K] X;
  vector[N] Y;
  vector[K-1] sd_x;
  real sd_y;
  real mean_y;
}

parameters {
  vector[K] b;
  real<lower=0> sigma;
}

transformed parameters{
  vector[N] mu;
  mu = X*b;
}

model {
  Y ~ normal(mu, sigma);
  b[1] ~ normal(mean_y, 2.5*sd_y);
  for(i in 1:(K-1)){
    b[1+i] ~ normal(0, 2.5*sd_y/sd_x[i]);
  }
  sigma ~ exponential(1/sd_y);
}

先程紹介したベクトルの演算をStan上で表現するために、vector型やmatrix型を使って表記します。注意点としては、transformed parametersで、行列とベクトルをかけ合わせるときの順番が、これまでのコードと違う点に気をつけてください。

ベクトル化を行うことによってfor文を減らし、可読性の高いコードにすることが可能になります。説明変数が何個増えても同じコードなので、再コンパイルの手間が格段に減らすことができます。

# 説明変数のmatrixを作成
X = baseball_df %>% 
  select(打率, 本塁打, 盗塁) %>% 
  mutate(one = 1) %>% #切片用に1だけの列を作る
  select(one, 打率, 本塁打, 盗塁) %>% 
  as.matrix()

stan_data = list(
  N = nrow(baseball_df),
  K = ncol(X),
  X = X
  Y = baseball_df$salary,
  sd_x = baseball_df %>% 
    select(打率, 本塁打, 盗塁) %>% 
    as.matrix() %>% 
    colMeans(),
  sd_y = sd(baseball_df$salary),
  mean_y = mean(baseball_df$打率),
)

stanmodel3 <- stan_model("2020_Stan_adcal/VMLM.stan")
fit_stan03 <- sampling(
  stanmodel3,
  data = stan_data,
  seed = 1234,
  chain = 4,
  cores = 4,
  iter = 2000
)

Stanにデータを入れる際に、説明変数のXの1列目には1を入れてmatrixにすることと、切片を含んだ説明変数の数（K）をStan側に渡してやる必要があります。

ベクトル化したコードでも通常の重回帰分析とほとんど同じような結果になりましたね。

おまけ：年俸がそもそも正規分布ではない

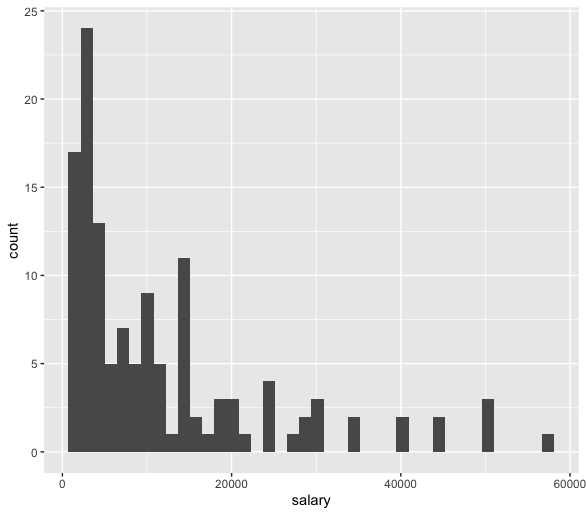
今回の記事ではStanで重回帰分析をするというのがメインだったため、年俸が正規分布ではないということを放置してきました。

上のヒストグラムは、今回対象になる選手の年俸のものですが、どう見ても正規分布ではありません。今まで放置してきましたが、どうやらこのまま正規分布と仮定して分析するのは難しそうです（今更）。

所得の分布状況は対数正規分布に従うという話があります。

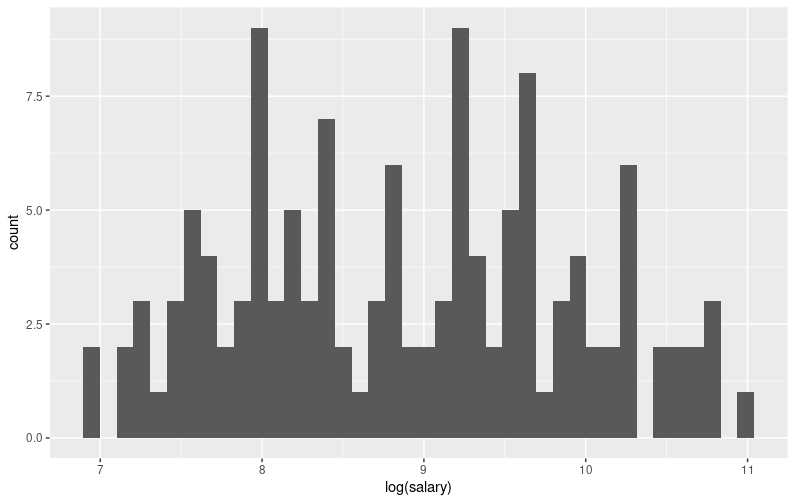
年俸を対数変換してみます。変換前よりも正規分布っぽくなりました。

Stanコード

対数正規分布を仮定したモデルは以下。「ソースを表示」をクリックするとコードが表示されます。WAICなどの情報量規準計算のためにtarget記法と、generated quantitiesを定義しています。

data {
  int<lower=0> N; //人数
  int<lower=0> K; //変数の数
  matrix[N, K] X;
  vector[N] Y;
  vector[K-1] sd_x;
  real sd_y;
  real mean_y;
}

parameters {
  vector[K] b;
  real<lower=0> sigma;
}

transformed parameters{
  vector[N] mu;
  mu = X*b;
}

model {
  target += lognormal_lpdf(Y | mu, sigma);
  target += normal_lpdf(b[1] | mean_y, 2.5*sd_y);
  for(i in 1:(K-1)){
     target += normal_lpdf(b[1+i] | 0, 2.5*sd_y/sd_x[i]);
  }
  target += exponential_lpdf(sigma | 1/sd_y);
}

generated quantities {
  vector[N] log_lik;
  vector[N] y_pred;
  for(n in 1:N){
    log_lik[n] = lognormal_lpdf(Y[n] | mu[n], sigma);
    y_pred[n] = lognormal_rng(mu[n], sigma);
  }
}

結果・モデル比較

モデル	回帰係数	平均値	95%信頼区間
正規分布	打率	94333.51	[39196.45~147364.60]
対数正規分布		129314.2	[1422.257~10638606]
正規分布	本塁打	585.29	[418.26~752.90]
対数正規分布		1.04	[1.03~1.06]
正規分布	盗塁	97.52	[-109.85~300.37]
対数正規分布		1.01	[0.99~1.03]

正規分布モデルと比べて、対数正規分布モデルの方は打率の95%信頼区間が範囲が広くなりすぎてしまい、本塁打や盗塁の効果がほとんどなくなってしまいました。打率1割で最大100億円…..

追記：対数正規モデルの結果はexp()で変換した値になります。

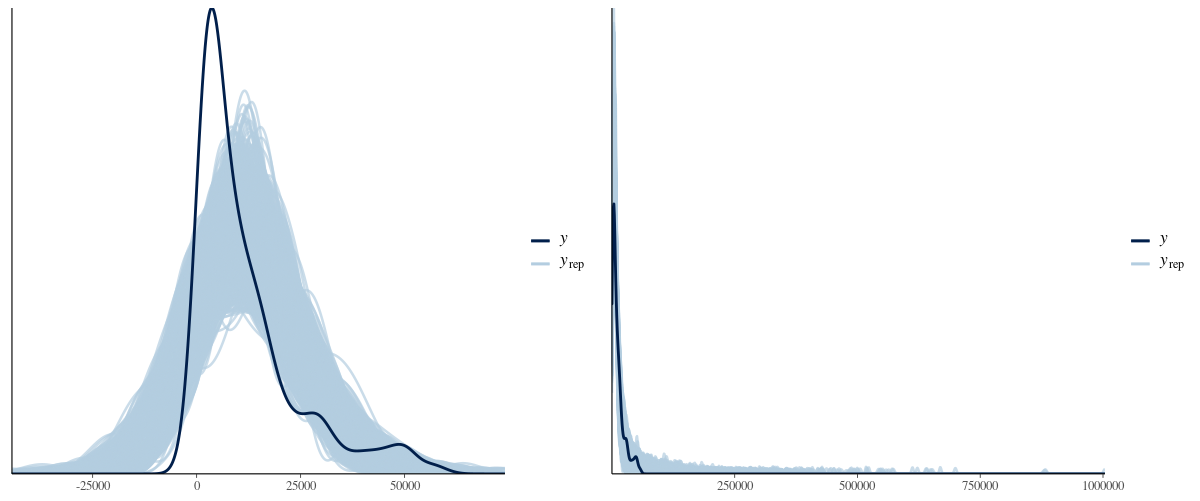
事後予測チェックの一貫として、今回のモデルから発生させた乱数をbayesplot::ppc_dens_overlay関数を使って描画してみました。どうやら対数正規分布の方が重なりは良さそうですね。実践が今回のデータ、色の薄い線が今回のモデルから発生させ乱数です。

モデル比較

モデル	正規分布	対数正規分布
WAIC	2696.2735	2546.0573
自由エネルギー	1357.456	1294.289

WAICと自由エネルギーを計算してみた所、対数正規分布モデルの方がどちらも低くなりました。

いかがでし(ry

今回は交絡しなさそうな変数として、打率・本塁打・盗塁数をチョイスしてみました。対数正規分布モデルは、情報量規準では良かったものの、打率の95%信頼区間が広くなってしまいました。野球の指標はたくさんあるので、対数正規分布モデルをベースに変数選択など、モデルの改善の余地はありそうです。

参考文献

Gelman et al. (2020) Regression and Other Stories (Analytical Methods for Social Research)

浜田・石田・清水（2019）社会科学のための ベイズ統計モデリング (統計ライブラリー　)
https://www.amazon.co.jp/dp/4254128428/ref=cm_sw_r_tw_dp_x_EavYFb50K9EA7

松浦 健太郎（2016）StanとRでベイズ統計モデリング (Wonderful R)
https://www.amazon.co.jp/dp/4320112423/ref=cm_sw_r_tw_dp_x_mnlYFbVD64NBN

持橋・大羽（2019）ガウス過程と機械学習 (機械学習プロフェッショナルシリーズ)
https://www.amazon.co.jp/dp/4061529269/ref=cm_sw_r_tw_dp_x_6nlYFb1HQGQEQ